Scaled Dot-Product Attention (SDPA)

Scaled Dot-Product Attention (SDPA)#

Overview#

Scaled Dot-Product Attention (SDPA) is introduced in [1] as the core operation of Transformer block which now becomes the backbone of many language models and generative models (BERT, Stable Diffusion, GPT, etc.).

The input of SDPA consists of query (Q), key (K), and value (V). The attention output is computed as:

\[attention(Q,K,V) = V \cdot softmax(\frac{QK^T}{\sqrt{d_k}})\]

\(d_k\) is the dimension size of K. Other notations used in the document:

  • N: the mini-batch size.

  • H: the number of multi-head.

  • S: the sequence length.

  • D_qk: the head size of query and key.

  • D_v: the head size of value.

SDPA patterns#

oneDNN supports SDPA and its optimization through Graph API [2] by defining the SDPA graph, getting partition from the graph, and optimizing the kernels underneath. In general, an SDPA pattern is defined as a directional acyclic graph (DAG) using oneDNN Graph API.

Floating-point SDPA for Inference#

oneDNN defines floating-point (f32, bf16, or f16) SDPA as follows. The blue nodes are required when defining an SDPA pattern while the brown parts are optional.

SDPA pattern

  1. The first MatMul calculates the dot products between Query and Key. See MatMul operation in Graph API.

  2. The Scale node is optional and is used to scale the output of the first MatMul with a scaling factor. It can be constructed by Multiply or Divide operation in Graph API. The scaling factor is given by users as an input of SDPA. \(\sqrt{d_k}\) in the formula is not considered as a part of the SDPA pattern because it is a constant.

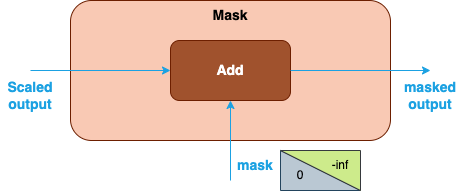
  3. The Mask node is optional and is used to apply an attention mask to the output of the previous Scale node. There are two types of masks that can be applied:

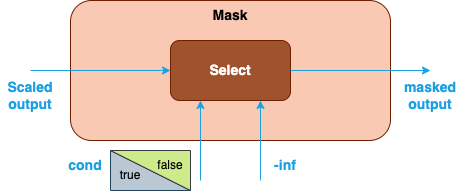
    1. Explicit user-generated mask: You can explicitly create a mask tensor and pass it to the library for the computation of SDPA. In this case, mask can be constructed by Add or Select operation in Graph API for different mask policies (for example, causal mask or padding mask). When the Add operation is used to apply the mask, the input mask is usually an upper triangular matrix with all the elements above the diagonal filled with -inf and zeroes elsewhere. The -inf entries will become zero probability after Softmax is applied in the next step. Alternatively, a Select operation may be used. In this case, the input is a boolean tensor (for example, with the boolean value set to true on and below the diagonal, and false above the diagonal). A false element in the mask forces the corresponding element of the scaled output to -inf, while a true element leaves it unchanged.

    SDPA-mask-1 SDPA-mask-2

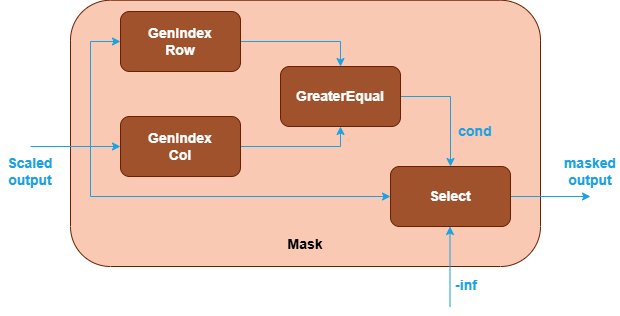
    1. Implicit library-generated mask: You can use the operations in the library to generate a mask by constructing a subgraph. Currently, Graph API supports generating an implicit causal mask (top-left or bottom-right aligned) using operations of GenIndex, Add. Subtract, GreaterEqual and Select.

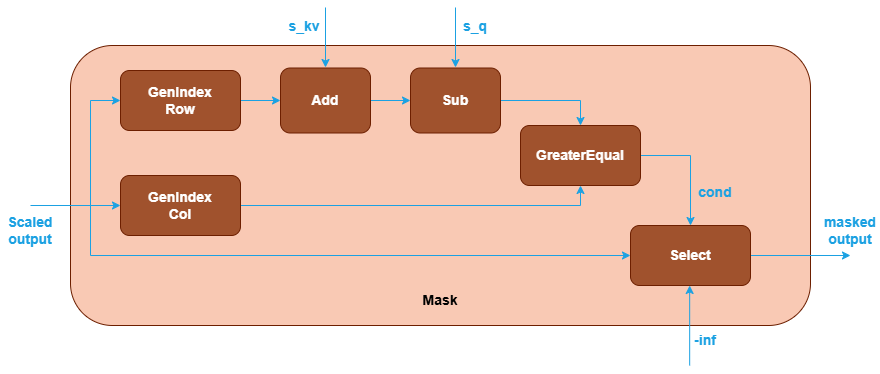
    SDPA-mask-3 SDPA-mask-4

  4. The SoftMax operation takes the masked output and transforms it into probabilities between 0 and 1. See SoftMax operation in Graph API.

  5. The second MatMul calculates the dot products between the probabilities after SoftMax and Value.

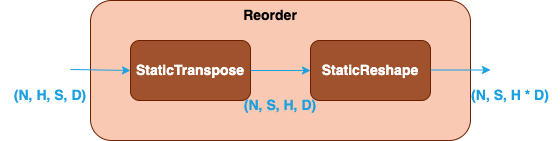
  6. The Reorder node is optional and used to reshape or transpose the attention output for cases where the attention output is transformed from shape (N, H, S, D_v) to (N, S, H, D_v) or (N, S, H * D_v). The node can be constructed by the combinations of StaticTranspose and StaticReshape operation in Graph API.

    SDPA-Reorder

Floating-point SDPA for Training Forward Propagation#

oneDNN defines floating-point (f32, bf16, or f16) SDPA for training forward propagation as follows. The blue nodes are required while the brown nodes are optional.

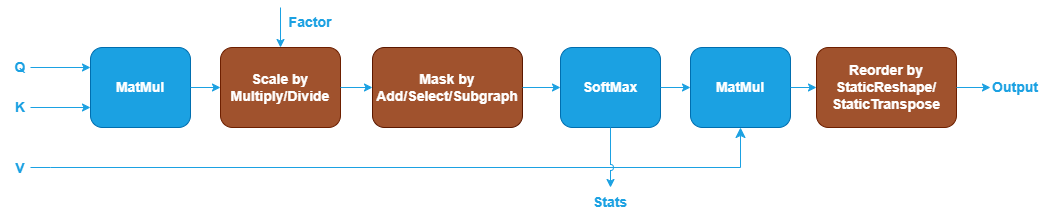
SDPA pattern

The only difference between the inference and training forward propagation patterns is that, for training forward propagation, the Stats output of the SoftMax operation is needed. See SoftMax in Graph API for more details.

Floating-point SDPA for Training Backpropagation#

oneDNN defines floating-point (f32, bf16, or f16) SDPA for training backpropagation as follows. The blue nodes are required while the brown nodes are optional.

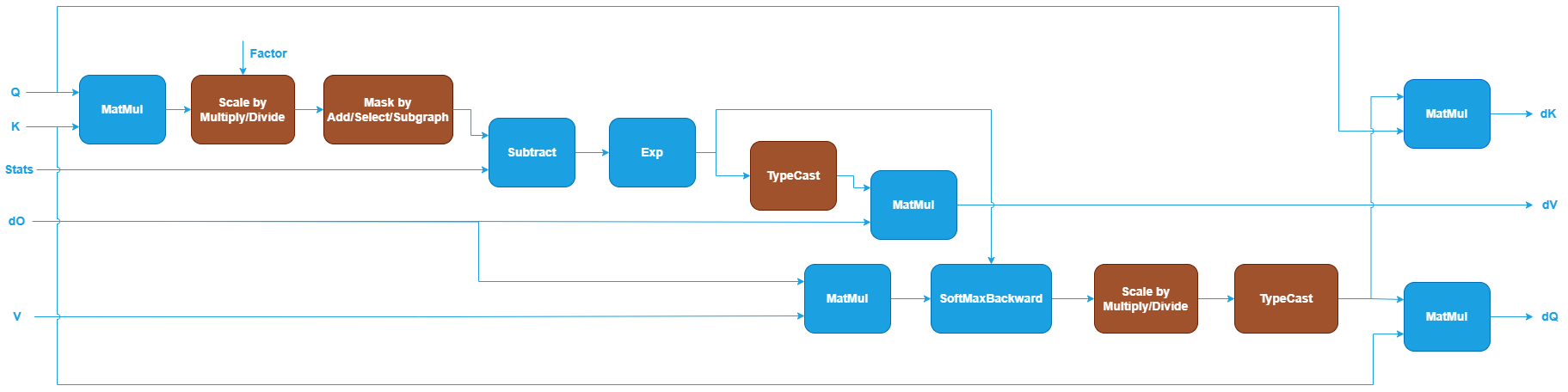
SDPA backward pattern

  1. The first MatMul computes the score between Query and Key, similar to inference and training forward propagation. See MatMul in Graph API.

  2. The Scale node is optional and scales the output of the first MatMul using a scaling factor. This can be implemented using Multiply or Divide in Graph API.

  3. The Mask node is optional and applies an attention mask to the output of the previous Scale node. For training backpropagation, only explicit user-generated masks are currently supported. The mask definition is the same as in inference and training forward propagation.

  4. The Subtract and Exp operations take the masked output and Stats as inputs and recover the probabilities computed by SoftMax in the training forward propagation. See Subtract and Exp in Graph API.

  5. The TypeCast and MatMul operations after Exp are used to compute the gradients with respect to Value. TypeCast is required for bf16 and f16 training scenarios. See TypeCast in Graph API.

  6. The MatMul takes the output gradients (dO) and the Value as inputs to compute the gradients of the probabilities.

  7. The SoftMaxBackward operation computes the gradients of the scaled output. See SoftMaxBackward in Graph API.

  8. The Scale node after SoftMaxBackward corresponds to the forward Scale node and is used to compute the gradients of the score.

  9. The TypeCast and two MatMul operations after the Scale node compute the gradients with respect to Query and Key, respectively. TypeCast is required for bf16 and f16 training scenarios.

Data Types#

oneDNN supports the floating-point SDPA pattern with data types f32, bf16, and f16. You can specify the data type via the input and output logical tensors’ data type fields for each operation.

oneDNN supports bf16 or f16 SDPA with f32 intermediate type. For inference and traing forward propagation, the Q, K and V tensors use bf16 or f16 data types, while the outputs of the first MatMul, Scale, Mask, and the input of SoftMax are in f32. Similarly, in training backpropagation, the Q, K, V, dO, dQ, dK and dV tensors use bf16 or f16, while the Stats input uses f32. The intermediate tensors are in f32, except those after TypeCast, which cast to bf16 or f16.

The definition of the data types and support status on different CPU and GPU platforms follow the general description in Data Types.

Implementation limitations#

  1. oneDNN primitive-based SDPA is implemented as the reference implementation on both Intel Architecture Processors and Intel Graphics Products. In this case, floating-point SDPA patterns are usually implemented with f32, bf16, or f16 matmul (with post-ops) and softmax primitives, while quantized SDPA patterns are implemented with int8 matmul (with post-ops) and f32, bf16, or f16 softmax primitives. The reference implementation requires memory to store the intermediate results of the dot products between Query and Key which takes \(O(S^2)\) memory. It may lead to out-of-memory error when computing long sequence length input on platforms with limited memory.

  2. The SDPA patterns functionally supports all input shapes meeting the shape requirements of each operation in the graph. For example, Add, Multiply, Divide, and Select operations require the input tensors to have the same shape or the shapes can be properly broadcasted based on the operation attribute.

  3. Dropout is currently not supported in SDPA training.

  4. CPU

    • Optimized implementation for inference is available for 4D Q/K tensors with shape defined as (N, H, S, D_qk) and V tensor with shape defined as (N, H, S, D_v).

    • Optimized implementation for inference is available for OpenMP runtime and Threadpool runtime on Intel Architecture Processors.

    • Specifically for OpenMP runtime, the optimized implementation requires N * H > 2 * thread number to get enough parallelism.

  5. GPU

    • Optimized implementation for inference is available for 4D Q/K tensors with shape defined as (N, H, S, D_qk) and V tensor with shape defined as (N, H, S, D_v) where D_qk equals D_v.

    • Optimized implementation for inference is available for f16 or bf16 SDPA with f32 intermediate data type and D <= 512 on Intel Graphics Products with Intel(R) Xe Matrix Extensions (Intel(R) XMX) support.

Example#

oneDNN provides an SDPA example demonstrating how to construct a typical floating-point SDPA pattern with oneDNN Graph API on CPU and GPU with different runtimes.

oneDNN also provides a MQA (Multi-Query Attention) example [3] demonstrating how to construct a floating-point MQA pattern with the same pattern structure as in the SDPA example but different head number in Key and Value tensors. In MQA, the head number of Key and Value is always one.

oneDNN also proides an SDPA with bottom-right implicit causal mask example demonstrating how to construct a floating-point SDPA pattern with implicit library-generated attention masks.

References#

[1] Attention is all you need, https://arxiv.org/abs/1706.03762v7

[2] oneDNN Graph API documentation, https://uxlfoundation.github.io/oneDNN/graph_extension.html

[3] Fast Transformer Decoding: One Write-Head is All You Need, https://arxiv.org/abs/1911.02150

Contents